“Si es todo ese tiempo, has arrojado ciento cincuenta y siete monedas... y consecutivamente ha salido cara... cincuenta y siete monedas consecutivamente, y todo lo que haces es jugar con tu comida”; extraído de Rosencrantz y Guildenstern han muerto, de Tom Stoppard
Si un jugador sin ventaja gana a la casa durante un largo periodo de tiempo, normalmente hay dos consecuencias importantes, especialmente si el jugador es un high roller. En primer lugar, el jugador probablemente pensará que tiene un sistema para ganar a la casa. En segundo lugar, el casino puede invertir importantes recursos a investigar un jugador honrado. En cualquier caso, se crea la ilusión de habilidad por falta de comprensión de la inevitabilidad estadística y de lo que se conoce como “largo plazo”. En esta publicación, voy a evaluar durante cuánto tiempo puede ganar a la casa un jugador de blackjack normal por pura suerte, ( a diferencia que en el programa de la ruleta de la suerte), y recuerdo que el significado de 888 tiene que ver con la suerte.
En general, un jugador de black jack que emplea una estrategia básica perfecta conseguirá una ventaja para la casa aproximada del 0,14 % al 0,65 %, según su juego (suponiendo que el jugador no esté lo suficientemente loco como para jugar a un juego de blackjack de 6:5). El jugador normal que tengo en mente comete pocos errores de estrategia básica, lo que da una ventaja para la casa del 1,0 %. Del mismo modo, las desviaciones estándares para la mayor parte de variaciones de blackjack van de 1,14 a 1,16 aproximadamente. Puesto que no se puede computar la desviación estándar de una estrategia y juego desconocidos, voy a establecer un valor medio de 1,15 como consenso. Asimismo, voy a suponer de forma indudablemente irrazonable que el jugador siempre apuesta la misma cantidad en cada mano.
La siguiente tabla de blackjack muestra la probabilidad de que el casino pierda ante el “jugador normal” descrito anteriormente después del número de manos dado, de 100 a 100.000 manos:
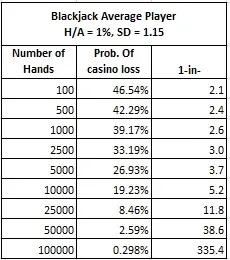
Después de 100 manos, el 46,5 % de estos jugadores normales ganarán a la casa. Después de 10.000 manos, el porcentaje que aún vence a la casa ha bajado al 19,2 %. A un ritmo de juego de 100 manos a la hora, casi uno de cinco jugadores con habilidades normales ganará a la casa después de 100 horas de juego. El sorprendente resultado, no obstante, es la última línea de esta tabla. Después de 100.000 manos, unas 1.000 horas de juego, un jugador de 335 seguirá ganando a la casa..
No hay nada que el casino pueda hacer con respecto a estos afortunados jugadores. Deben existir simplemente por probabilidad. Ningún tipo de “compensación” puede cambiar esta inevitabilidad estadística. En un gran casino, habrá bastantes jugadores que parecen no agotar su suerte más allá de toda razón. Si resulta que uno de estos jugadores es un high roller, la cosa se pone fea. A menudo, se invierten valiosos recursos al investigar al jugador. A veces, el casino simplemente expulsa al jugador sin una buena razón añadiendo algo del tipo “no podemos ganarle”. Generalmente, no hay argumento lógico que sea valga con la dirección cuando se enfrentan a un jugador tal. Piensan que resultados futuros del jugador serán similares a sus resultados pasados o, en otras palabras, esperan que este jugador siga ganando.
En cambio, no puedo decirte cuántas veces me ha dicho alguien que un familiar, amigo o colega suyo es un “profesional” que siempre gana a la casa. He dejado de dudar de estas personas; seguro que están en lo cierto. Su compañero ha ganado a la casa durante el transcurso de cuentos de horas. Lo molesto de la situación, sin embargo, llega cuando estos jugadores escriben libros, publican en foros o alardean públicamente de sus conocimientos y habilidades. Normalmente, ofrecen argumentos sin solidez sobre cómo consiguieron sus logros y defenderán su posición con burlas y evasivas. Ningún argumento convencerá a este tipo de jugador de que solo es uno más de esos afortunados que solo existen en virtud del modelo probabilístico para el juego.
La siguiente tabla muestra el número de manos necesario para alcanzar cierta confianza en ganar al jugador. He incluido los resultados para el jugador normal que consideramos antes y para el jugador de estrategia básica perfecta que participa en un juego de doble baraja estándar:

Por ejemplo, considera la entrada que aparece debajo de 90 % que se corresponde con el jugador genérico. Esta tabla muestra que se necesitan 21.720 manos antes de que el casino tenga un 90 % de probabilidades de ganar al jugador medio. Puesto de otro modo, el 10 % de todos los jugadores genéricos seguirán ganando a la casa después de 21.720 manos. De la misma forma, después de 126.293 manos, el casino tendrá una probabilidad del 99,9 % de ganar al jugador medio. En otras palabras, un jugador de 1.000 seguirá ganando a la casa después de 126.293 manos simplemente por probabilidad. Si resulta que ese jugador es un high roller, seguramente supondrá un problema de seguridad de juego y de gestión importante para el casino.
Ahora, considera el jugador de estrategia básica perfecta que aparece en la fila superior. En este caso, el número de manos necesario para conseguir varios niveles de confianza aumenta drásticamente. Ahora son necesarias 145.298 manos para tener un 90 % de confianza en ganar a este tipo de jugador. Para tener el 99 % se necesita la friolera cantidad de 478.480 manos. Dicho de otro modo, después de 478.480 manos, ¡un jugador de estrategia básica perfecta de 100 seguirá ganando a la casa! Para la mayoría de jugadores son más manos de blackjack de las que jugarían en toda su vida. En otras palabras, si un jugador utiliza una estrategia básica perfecta, puede no haber previsión razonable a largo plazo de ganar al jugador.
De todos los jugadores que recibe un casino, habrá un número importante de ganadores a largo plazo, incluso entre los jugadores con habilidades normales. Para ver esta inevitabilidad estadística desde otra perspectiva, he llevado a cabo una simulación de 25 jugadores de estrategia básica perfecta. En esta simulación, he supuesto que el juego sería 6D (el jugador puede doblar solo en 6 duro), H17 (el crupier debe sacar carta en 17 blando), DOA (el jugador puede doblar en otras dos cartas) y DAS (el jugador puede doblar después de una división) con una ventaja para la casa del 0,61 %. Cada jugador ha jugado 100.000 manos y he rastreado y trazado sus resultados a lo largo de su recorrido. La siguiente imagen muestra los resultados de esta simulación (haz clic en la imagen para agrandarla):
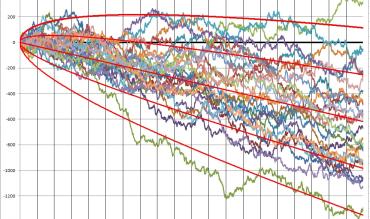
La línea roja recta que aparece en el medio indica la “pérdida teórica” de los jugadores. Esta línea representa la cantidad que espera ganar el casino del jugador después del número de manos dado. Las líneas rojas curvas que aparecen por encima y por debajo de esta línea recta indican las desviaciones estándares +2, +1, -1, y -2 de las teóricas, respectivamente. El resultado actual para cada uno de los 25 jugadores, en función del número de manos jugadas, se traza de izquierda a derecha en cuanto a “unidades” ganadas o perdidas.
Ten en cuenta que hay un jugador de esos 25 que terminó por delante después de esas 100.000 manos (véase la línea verde superior). Este jugador quedó por delante por unas 300 unidades. Si su unidad fuera 10 $, su ganancia sería de 3.000 $ y pasaría desapercibido. Pero si su unidad fuera 1.000 $, su ganancia sería de 300.000 $ y se convertiría en el centro de la investigación. ¿Cómo se ve a sí mismo este jugador? Probablemente, tanto él como sus amigos estarán convencidos de que es un jugador habilidoso, aunque no tenga ni idea de qué habilidad es la que posee.
Por otra parte, el jugador verde de la parte inferior ha tenido muy mala suerte puesto que sus resultados están aproximadamente dos desviaciones estándares por debajo de lo normal. Después de 100.000 manos, este jugador ha perdido alrededor de 1.300 unidades. Con una apuesta de 10 $, este jugador ha perdido alrededor de 13.000 $. Si este jugador es un high roller con una unidad de 1.000 $, habría perdido alrededor de 1,3 millones. ¿Cómo se ve a sí mismo este jugador? Es un gran perdedor de blackjack que está harto de ver cómo los demás jugadores son mejores que él, pero que es incapaz de saber qué está haciendo mal.
Hubo otro jugador que terminó casi igualado después de 100.000 manos. Otros tres jugadores terminaron con una pérdida de al menos 1.000 unidades en esta simulación. Inventar líneas narrativas desde la perspectiva del casino y desde la perspectiva del jugador para cada uno de ellos resulta un ejercicio interesante.
A continuación vemos a 25 jugadores más (haz clic en la imagen para agrandarla, como antes):
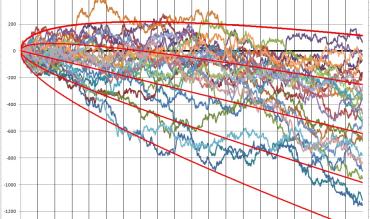
No hay nada que pueda hacer el casino con respecto a la variedad de resultados que obtienen los jugadores. Del mismo modo, los jugadores no pueden hacer nada para elegir su línea. Algunos jugadores tendrán buena suerte y otros tendrán mala suerte. El casino no debería excluir a los ganadores. Los ganadores no deberían engañarse a sí mismos.
Cuando mostré estas simulaciones a una vicepresidenta sénior de marketing para un importante casino internacional, me preguntó si no era inevitable que cada línea convergiera en algún momento con la línea recta que había en el centro del gráfico. Creía que, a largo plazo, los resultados de cada jugador deberían ser prácticamente iguales a su pérdida teórica. En otras palabras, los ganadores perderían y los perdedores ganarían. La respuesta fue no. Entonces me preguntó si los jugadores ganadores o perdedores seguirían perdiendo/ganando a un ritmo similar. De nuevo, la respuesta fue no. No son solo los juegos de mesa y la vigilancia los que a veces fallan el golpe.
En adelante, los resultados futuros son independientes de los resultados pasados. Nada de lo que haya hecho un jugador en el pasado tiene relevancia alguna en los resultados de este jugador en el futuro. Esto es así para los jugadores normales y para los jugadores de estrategia básica. Después de 100.000 manos, cada jugador está sujeto a las mismas probabilidades prospectivas que los demás jugadores. Las cartas no tienen memoria. La falacia de juegos de azar de que el pasado es relevante para el presente forma parte de conexiones evolutivas erróneas de la mente humana.


