Over/Under (O/U) es un nuevo juego de mesa aprobado recientemente y que empieza a recibir apuestas nacionales. Se ha debatido bastante en los foros de mensajes de juegos con ventaja sobre el conteo de cartas en este juego y una apuesta complementaria asociada (consulta este hilo en wizardofvegas.com y este hilo en blackjacktheforum.com). En esta publicación, analicé el conteo de cartas de la apuesta complementaria de bonificación que acompaña a este juego. En esta publicación, abordaremos el conteo de cartas del juego principal y también el enfoque adoptado por un equipo de dos personas para jugar contra el juego principal y la apuesta complementaria de bonificación.
Según la documentación disponible proporcionada por el inventor del juego (informe de Joseph Shipman e informe de Donald Catlin), el juego O/U se reparte desde un dispensador que contiene cuatro, seis u ocho barajas de cartas comunes. El juego se basa en el valor total de tres cartas, que puntúan del siguiente modo:
- 2, 3, 4, 5, 6, 7, 8, 9, 10 tienen su propio valor.
- La jota, la reina y el rey tienen un valor de 10.
- El as tiene un valor de 11.
En otras palabras, el valor total de las tres cartas se calcula del mismo modo que en el blackjack, salvo por los ases que siempre valen 11.
Para jugar al O/U, el jugador empieza realizando una apuesta ante de una unidad. Después, recibe una carta abierta. Tras examinar dicha carta, el jugador tiene tres opciones. Puede retirarse, realizar una apuesta arriba (Over) o hacer una apuesta (Under). Si realiza una apuesta arriba o una apuesta abajo, estas deben ser iguales que la apuesta ante..
Si el jugador se retira, pierde su apuesta ante y no podrá volver a participar en la mano. En caso contrario, el jugador recibe dos cartas más. En ese caso, el jugador tendrá un total de tres cartas, tal y como se describió anteriormente. La mano se resuelve del siguiente modo:
Si el jugador realiza una apuesta arriba:
- Si el valor total de sus tres cartas es 24 o más, el jugador gana y recibe dinero seguro por su apuesta ante y su apuesta arriba.
- Si el valor total de sus tres cartas es 23 o menos, el jugador pierde su apuesta ante y su apuesta arriba.
Si el jugador realiza una apuesta abajo:
- Si el valor total de sus tres cartas es 17 o menos, el jugador gana y recibe dinero seguro por su apuesta ante y su apuesta arriba.
- Si el valor total de sus tres cartas es 18 o más, el jugador pierde su apuesta ante y su apuesta arriba.
La estrategia del jugador se basa en un dato: el valor de su primera carta. Es obvio que si el valor de dicha carta es lo suficientemente alto, querrá realizar la apuesta arriba, y si es lo suficientemente bajo, querrá realizar la apuesta abajo. Lo que no es tan obvio es si el jugador debería retirarse en algún momento.
La siguiente tabla muestra el análisis combinatorio para las apuestas arriba/abajo junto con el valor esperado para cada estrategia:
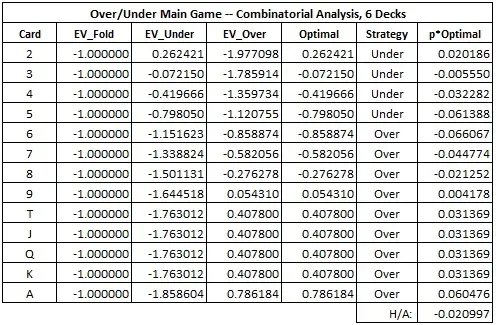
Concretamente, la ventaja de la casa para las apuestas arriba/abajo es del 2,0997 %.
La estrategia es extremadamente sencilla. Si el valor de la primera carta que recibe el jugador es 2, 3, 4 o 5, el jugador debería realizar la apuesta abajo. Si el valor de la primera carta es 6 o más, el jugador debería realizar la apuesta arriba. El jugador nunca debería retirarse.
Dado que el jugador nunca se retira, podríamos estar tentados a decir que el jugador siempre apostará dos unidades y, por tanto, la ventaja de la casa será la mitad del 2,0997 %. En otras palabras, si no se comprende el término “ventaja de la casa”, se podría llegar a afirmar erróneamente que la ventaja es del 1,0498 %. Lo cual sencillamente no es cierto. Este juego no exige que se realice una apuesta inicial de dos unidades; exige una apuesta de una unidad. Por tanto, la apuesta de la casa debería basarse solo en esa apuesta.
Debería resultar obvio que en este juego se pueda aplicar el conteo de cartas. Lo que no resulta tan obvio es decidir si las apuestas arriba y abajo deberían valorarse de manera independiente. Al observar la tabla anterior vemos que solo el 2 ofrece un valor esperado positivo para la apuesta abajo. En cambio, el 9, el diez, la jota, la reina, el rey y el as ofrecen un valor esperado positivo para la apuesta arriba. Dicho de forma sencilla, la apuesta arriba es de donde procede la mejor parte de la ganancia del jugador. Puede que se gane poco dinero con el conteo de cartas de la apuesta baja, pero no hablaremos de ese tema ahora.
Para que este análisis resulte aún más sencillo, voy a asumir que el contador de cartas nunca cambia su estrategia de juego. No importa el conteo, siempre realizará la apuesta arriba con un 6 o más, y la apuesta abajo con un 2, 3, 4 o 5. El contador nunca se retirará. La única cosa que el contador cambiará con el conteo será el tamaño de su apuesta. En este supuesto, la siguiente tabla indica el efecto de eliminación (EOR, por sus siglas en inglés) de cada carta, junto con un sistema de conteo de cartas basado en estos EOR:
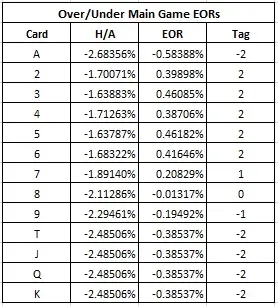
El sistema de conteo de cartas recomendado tiene los siguientes valores:
- 2, 3, 4, 5, 6 = 2
- 7 = 1
- 8 = 0
- 9 = -1
- A, T, J, Q, K = -2
Se trata de un sistema de conteo de cartas equilibrado y directo. La correlación de apuestas es del 0,990, lo cual es bastante fuerte. Este sistema de conteo de cartas concede mayor importancia a las cartas que ofrecen manos arriba ganadoras, mientras que penaliza a las cartas que es probable que ofrezcan manos bajas ganadoras. Básicamente, este sistema excluye la parte “baja” del Over/Under.
La siguiente tabla presenta los resultados de una simulación de cien millones (100.000.000) de dispensadores para seis barajas, con la carta de corte en 260, en los que el jugador utilizó el sistema de conteo de cartas anterior. Supongamos que el jugador siempre realizó una apuesta arriba con un 6 o más y una apuesta abajo con un 5 o menos:
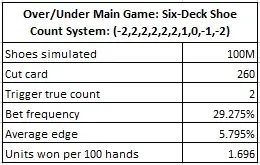
Concretamente, fíjate en que el contador de cartas tiene la ventaja cuando el conteo real es +2.
El índice de ganancia que ofrece esta tabla puede resultar confuso. Normalmente analizo el conteo de cartas en el contexto de las apuestas complementarias, cuando el jugador no necesita jugar la apuesta complementaria de cada mano. En este juego, el jugador puede que no pueda entrar y salir en un momento determinado, solo realizar apuestas cuando tenga la ventaja. Puede que tenga que jugar manos cuando la casa tenga la ventaja. Por tanto, resulta razonable valorar su índice de ganancia cada vez que juega una mano. Para ello, es necesario tener en cuenta la ventaja media que tiene el casino cuando el conteo real es inferior a +2.
Estos son los valores cuando la casa vence al jugador (conteo real inferior a +2):
- El conteo real es inferior a +2 en el 70,725 % de las manos.
- De media, cuando el conteo real es inferior a +2, la casa tiene una ventaja del 5,367 % sobre el jugador.
Para ver cómo encaja todo esto, voy a poner un ejemplo realista. Imagina que Over/Under se juega en un casino en el que el mínimo de la mesa es 5 $ y el máximo 100 $. El contador puede decidir si quiere utilizar un margen de apuesta de 10 a 1 con una apuesta máxima de 100 $. Para ello, el contador apuesta 10 $ cuando el conteo es inferior a +1 y apuesta 100 $ cuando el conteo es +1 o superior.
Entonces, de cada 100 manos, de media:
- El jugador apuesta 10 $ en 70,725 de las manos con una ventaja de la casa del 5,367 %. De este modo, pierde de media 10 $*70,725*5,367 % = 37,96 $.
- El jugador apuesta 100 $ en 29,275 de las manos con una ventaja del jugador del 5,795 %. De este modo, gana de media 100 $*29,275*5,795 % = 169,64 $.
En otras palabras, el contador pierde 37,96 $ por cada 100 manos de sus apuestas de 10 $ y gana 169,64 $ por cada 100 manos de sus apuestas de 100 $. Al restarlos, el resultado global del contador es 131,68 $ de ganancia por cada 100 manos.
En comparación, un jugador medio de blackjack que utilice el conteo de cartas normal con un dispensador para seis barajas y que tenga una apuesta máxima de 100 $ ganará unos 22 $ por cada 100 manos. Básicamente, para el jugador con una apuesta máxima de 100 $, el conteo de cartas Over/Under será casi seis veces tan rentable como el conteo de cartas en el blackjack normal.
Esto puede resultar incluso más lucrativo si dos contadores de cartas juegan juntos. De nuevo, pensemos en una apuesta máxima de la mesa de 100 $ en el juego Over/Under principal. Además, pensemos en una apuesta máxima de 25 $ en la apuesta de bonificación de Over/Under. Uno de los contadores (llamémosle “Joe”) mantendrá el conteo Over/Under descrito anteriormente. El otro contador (llamémosle “Fred”) mantendrá el conteo de la apuesta de bonificación. Cuando Joe realiza una apuesta en el juego principal de 100 $, Fred hace lo mismo y también realiza una apuesta en el juego principal de 100 $. Cuando Fred realiza una apuesta de 25 $ a la apuesta de bonificación, Joe hace lo mismo y también realiza una apuesta a la apuesta de bonificación de 25 $. De este modo, tanto Joe como Fred obtienen el índice de ganancia completo gracias al conteo de ambas apuestas.
La siguiente tabla resumen el debate anterior:
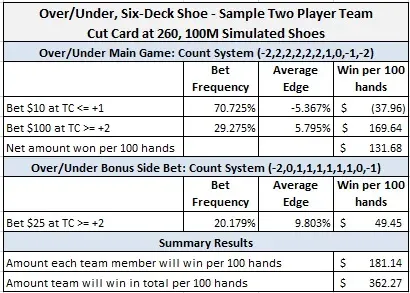
Este análisis no se centra en las miles de configuraciones posibles del juego, incluido el número de barajas utilizadas, la posición de las cartas de corte, los máximos de las mesas y los márgenes de apuesta. Se podría investigar diferentes sistemas de conteo. Tal vez una parte de la apuesta arriba se pueda seleccionar con un conteo complementario. Tal vez exista un índice de “estrategia” para las decisiones en el Over/Under. Tal vez se pueda aplicar un único conteo conjunto en la apuesta principal y la apuesta de bonificación. Todo ello puede hacerse, por supuesto, pero el ejemplo anterior debería ser suficiente como explicación.
En mi opinión, Over/Under es vulnerable al conteo de cartas. Cualquier casino que lo ofrezca debería prestar atención a la posibilidad de aplicar el conteo de cartas en el juego principal, la puesta complementaria de bonificación o ambas jugando en equipo. La solución más sencilla consiste en repartir en el Over/Under desde un barajador continuo. Esta es mi recomendación más rentable.


