Aviso: Todos los consejos dados en este artículo tienen un carácter meramente informativo basado en bibliografía sobre juegos de azar. Sin embargo ninguno de estos consejos garantiza ni es un elemento determinante para el éxito en la actividad del juego analizado. En nuestro blog tratamos tematicas relacionadas con el mundo de los juegos y los contenidos son informativos y no significa que tengamos disponible el juego, producto, utensilio, accesorio, etcétera…del que habla el articulo.
Cuando escuché a Don Johnson (D. J.) hablar el pasado martes en la World Game Protection Conference, esperaba que atribuyese sus ganancias en blackjack al resultado de sumar un poquito de juego con ventaja con mucha suerte. Sin embargo, con su explicación sobre cómo jugar en las carreras de caballos, pocas dudas quedaban de su habilidad como uno de los mejores jugadores con ventaja del mundo. Cuando D. J. mencionó la ventaja de la casa exacta de uno de los juegos de blackjack en los que participó (0,263 %), acabó con todo rastro de duda.
Si aún no lo has hecho, te recomiendo que veas este vídeo producido por Bloomberg [añadido en enero de 2014]. Te transmite una buena sensación sobre qué tipo de persona es Don Johnson. Objetivamente, es mejor que la mayoría de los artículos de consumo habitual sobre juegos de azar, pero se sigue quedando algo corto al dar explicaciones sobre lo que realmente ocurrió.
Como explicó D. J., el trato que negoció en Atlantic City incluía los siguientes términos:
- D. J. estableció un crédito de 1.000.000 $ con el casino.
- Si D. J. perdía 500.000 $ en un día, podía dejar de jugar y recibir una devolución del 20 % de su pérdida.
- Podía realizar una apuesta máxima de 100.000 $. En algunos sitios, este máximo era 50.000 $.
En el mundo de los casinos, suele ocurrir que la gente entiende algo como “obvio”, cuando en realidad no lo es y normalmente es un error. Así fue después de la masacre de D. J. Casi todo el mundo dio por sentado que la mejor estrategia era que D. J. jugara hasta jugar o perder 500.000 $ y dejar de jugar ese día. Esta “estrategia” parece lógica pura (si no utilizas ningún tipo de lógica). Pero, curiosamente, no representaba el curso real de los acontecimientos en el juego de D. J. De hecho, D. J. jugó mucho más durante los días en los que obtenía ganancias de lo que dictaba esta “estrategia”. En los días en los que perdía, D. J. aguantaba pérdidas de más de 500.000 $. Decidí simular las circunstancias del juego de D. J. para determinar los puntos de parada óptimos. Lo que descubrí demostraba que D. J. tenía razón al seguir jugando más allá de los míticos “puntos de parada” de +/-500.000 $...
En primer lugar, establecí el juego al que se estaba jugando. Para los mejores jugadores, las siguientes reglas son estándares en un juego con mazo:
- Seis barajas
- El crupier se planta en 17 blando
- El jugador puede doblar en cualquiera de las dos primeras cartas
- El jugador puede doblar después de dividir
- El jugador puede volver a dividir ases
- El jugador puede volver a dividir en cuatro manos
- Abandono tardío.
Así es como enfocaba D. J. el juego. Pudo haber jugado con otro conjunto de reglas, pero D. J. no mencionó nada al respecto.
A continuación, diseñé un programa informático que me permitía realizar una simulación Montecarlo para averiguar las posibles estrategias de parada que podía utilizar D. J. El resultado de esta simulación dio un juego con mazo en el que se utilizó una carta de corte con las reglas enumeradas anteriormente. Es algo un poco misterioso, pero cuando el crupier utiliza una carta de corte, la ventaja pasa ligeramente a estar de parte de la casa (lo que se conoce como el “efecto de la carta de corte”). En el caso de este juego, la ventaja era de aproximadamente el 0,29 % con una carta de corte. Si quieres saber más, consulta el apéndice n.º 4 sobre blackjack del sitio web Wizard of Odds.
Entonces, ejecuté 16 simulaciones para varias estrategias de parada (desde una ganancia de 500.000 $ hasta una ganancia de 2.000.000 $) para determinar el punto de parada óptimo (redondeado a 100.000 $). Cada una de las 16 simulaciones consistía en representar a un millón de jugadores (100.000.000) que utilizaban esa estrategia de parada y en obtener la media de sus resultados. El resultado del programa incluía la ventaja para el jugador sobre la casa, la ganancia esperada para el jugador y el promedio de manos del jugador.
La siguiente tabla ofrece los resultados del análisis de los puntos de parada para D. J. con una apuesta fija de 100.000 $:
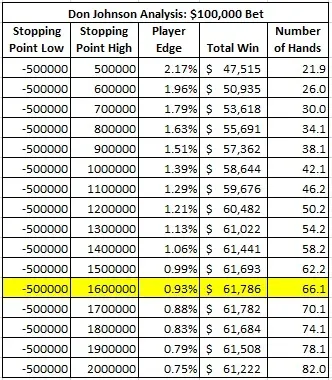
Estos resultados demuestran que el punto de parada óptimo para D. J. era una ganancia de 1.600.000 $ (no de 500.000 $, como todo el mundo pensaba). D. J. estaba jugando con una ventaja general del 0,93 % sobre la casa. La ganancia esperada de D. J. era de 61.786 $. El número de manos esperado era 66,1.
La siguiente tabla ofrece los resultados del análisis de los puntos de parada para D. J. con una apuesta fija de 50.000 $:
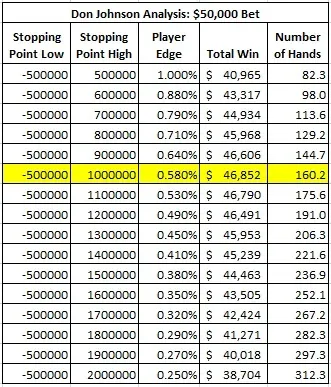
En este caso, el punto de parada óptimo para D. J. era una ganancia de 1.000.000 $. D. J. jugaba con una ventaja general de 0,58 % sobre la casa. La ganancia esperada de D. J. era de 46.852 $. El número de manos esperado era 160,2.
A estas alturas, a ti también puede sorprenderte la credibilidad de parar con una pérdida de 500.000 $ y harías bien. De nuevo, la creencia popular es errónea. Después de haber perdido 500.000 $, D. J. está jugando fundamentalmente con un descuento del 20 % sobre cada apuesta que realiza, puesto que ya no tiene que reunir los requisitos para el descuento de pérdidas. La única limitación residía en que D. J. debía mantener el dinero suficiente para doblarse o dividir (200.000 $ con una apuesta de 100.000 $ y 100.000 $ con una apuesta de 50.000 $). En su charla, D. J. dejó claro que en varias ocasiones perdió más de 500.000 $ antes de dejar de jugar ese día. ¿Crees que D. J. sabía lo que hacía?
Volví a realizar el análisis dado en las tablas anteriores con dos grados de libertad (puntos de parada alto y bajo). En los siguientes resultados, asumí que había exactamente 1.000.000 $ en el cajero. En mi siguiente artículo sobre Don Johnson, quité también este requisito para averiguar el índice de ganancias óptimo según sus puntos de ganancia/pérdida y abandono.
A continuación se enumeran los puntos de parada óptimos y demás datos relevantes al apostar 100.000 $ por mano, con 1.000.000 $ en el cajero:
- Parar cuando la cuenta actual tenga menos de 200.000 $ (se han pedido más de 800.000 $).
- Parar al jugar 2.000.000 $.
- La ventaja del jugador es del 0,63 %.
- TEl promedio de ganancia total es 85.800 $.
- El promedio total de manos es 136,9.
A continuación se enumeran los puntos de parada óptimos y demás datos relevantes al apostar 50.000 $ por mano:
- Parar cuando la cuenta actual tenga menos de 100.000 $ (se han pedido más de 900.000 $).
- Parar al jugar 1.200.000 $.
- La ventaja del jugador es del 0,34%.
- El promedio de ganancia total es 59.900 $.
- El promedio total de manos es 350,3.
Existe otro enfoque para este análisis. Supongamos que D. J. juega sin puntos de parada y que en su lugar predetermina el número de manos que va a jugar al día y lo mantiene pase lo que pase. Al estar sujeto a un número de manos fijo, ¿cuántas manos maximizarían las ganancias de D. J.? En este caso, el análisis es casi exacto. La metodología se encuentra descrita en el capítulo n.º 15 del libro “Casino Operations Management” (Gestión de operaciones del casino). Anteriormente, había escrito una versión de este análisis para mi propio trabajo de asesoría, así que la utilicé para esta simulación de D. J. Simplemente introduje sus parámetros de devolución de pérdida y probé manualmente con varios números de manos hasta encontrar su ganancia máxima.
La siguiente tabla ofrece el punto de parada de “número de manos” óptimo para una apuesta de 100.000 $:
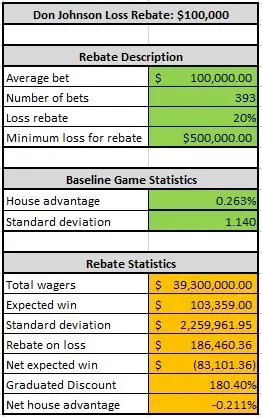
Con una apuesta fija de 100.000 $ y un punto de parada de “número de manos”, D. J. debería jugar exactamente 393 manos al día. En este caso, el promedio de ganancia de D. J. por día sería 83.101 $, con una ventaja media de 0,211 % sobre la casa.
La siguiente tabla ofrece el punto de parada de “número de manos” óptimo para una apuesta de 50.000 $:
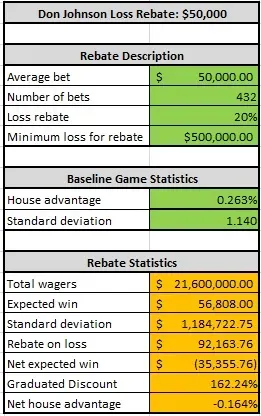
Con una apuesta fija de 50.000 $ y un punto de parada de “número de manos”, D. J. debería jugar exactamente 432 manos al día. En este caso, el promedio de ganancia de D. J. por día sería 35.356 $, con una ventaja media de 0,164 % sobre la casa.
Para terminar de explicar cómo derrotó D. J. a la casa, no bastan estos datos. Durante su charla, D. J. explicó que consiguió 50.000 $ en dinero para jugar al día. Además, declaró que construyó una personalidad extremadamente beligerante e insufrible que llevaba al límite a los crupieres y al personal. Afirmó que esto ayudaba a hacer que el crupier cometiese errores y a que el personal tomara decisiones subjetivas. Calculó que, gracias a su “actuación”, había ganado tres unidades adicionales al día. Esto ascendía a 150.000 $ o 300.000 $, según el tamaño de su apuesta (confío en la palabra de D. J. en esto porque no puedo verificar estos números).
Por último, D. J. reveló que tenía compañeros de equipo secretos. Añadió que los límites de la mesa iban desde un mínimo de la mesa de 100 $ hasta su apuesta fija (50.000 $ o 100.000 $). Cuando el mazo se volvía suficientemente negativo, simulaba un berrinche a tenor de su actuación y dejaba de jugar. Entonces, sus compañeros de equipo acababan con el resto del mazo negativo. De esta forma, su juego fue igual al de un contador de cartas que distribuía de forma efectiva sus apuestas desde 100 $ hasta la apuesta máxima de D. J. de 50.000 $ o 100.000 $. Calculé las ganancias adicionales diarias de D. J. por conteo de cartas de blackjack utilizando los valores de acuerdo con este análisis:
- Con una apuesta de 50.000 $, D. J. tenía una ganancia teórica de aproximadamente 26.000 $ al día con el conteo de cartas.
- Con una apuesta de 100.000 $, D. J. tenía una ganancia teórica de aproximadamente 21.000 $ al día con el conteo de cartas.
Si se tienen en cuenta todas estas fuentes de ingresos, las ganancias diarias esperadas de D. J. con una apuesta fija de 50.000 $ eran aproximadamente:
- 60.000 $ + 50.000 $ + 3 x 50.000 $ + 27.000 $ = 287.000 $.
Las ganancias diarias esperadas de D. J. con una apuesta fija de 100.000 $ eran aproximadamente:
- 86.000 $ + 50.000 $ + 3 x 100.000 $ + 21.000 $ = 457.000 $.
En el artículo de la revista The Atlantic, daba la impresión de D. J. había tenido una suerte increíble al jugar con la rapidez con la que lo hizo. Ahora está bastante claro que la suerte tuvo poco que ver en esto. D. J. manipuló las “condiciones de mercado” que se le ofrecían para crear las condiciones con las que se coronaría ganador. D. J. consultó a sus asesores matemáticos para que le ayudaran a crear una estrategia con la que optimizar su retorno de acuerdo con los parámetros de juego disponibles. Entonces, D. J. llevó a cabo su plan con un extraordinario talento que abarcaba todos los matices tácticos y estratégicos.
Presenciar tal nivel de habilidad, planificación y ejecución, sin importar en qué lado de las mesas juegues, supone una lección de humildad. Los casinos de Atlantic City no tenían nada que hacer.


